Bruchrechnung
| Website: | Herzlich willkommen! |
| Kurs: | Bruchrechnung |
| Buch: | Bruchrechnung |
| Gedruckt von: | Gast |
| Datum: | Dienstag, 10. März 2026, 03:39 |
Dieses Kapitel enthält die folgenden Themen:
Bruchrechnung - Erklärungen
Bei den Zahlenbereichen hatten wir schon gesehen, dass es nicht nur ganze Zahlen gibt, sondern auch gebrochene. In diesem Kapitel schauen wir uns diese Zahlen und den Umgang mit ihnen etwas genauer an.
Was ist ein Bruch?
Bei einem Bruch \(\dfrac {p}{q}\) heißt \(p\) Zähler und \(q\) Nenner.
Der Bruchstrich steht dabei für eine Division. Auch wenn für \(p\) und \(q\) grundsätzlich beliebige reelle Zahlen eingesetzt werden dürfen, ist es üblich, in Brüchen ganze Zahlen zu verwenden, also \(p,q \in \mathbb{Z}\). Immer gilt, dass der Nenner \(q \neq 0\) sein muss, da durch \(0\) nicht geteilt werden darf!
Aufgrund der Rechenregeln für die Division gilt:
- \(\dfrac{p}{p}=1\) für alle Zahlen \(p \in \mathbb{R}\backslash_{ \{0\} }\)
- \(\dfrac{-3}{4}=\dfrac{3}{-4}=-\dfrac{3}{4}\)
- \(\dfrac{3}{4}=\dfrac{+3}{+4}=\dfrac{-3}{-4}=+\dfrac{3}{4}\)
Zur Schreibweise: Es ist egal, ob man \(4 \cdot \dfrac{3}{10}\) oder \(\dfrac{3}{10} \cdot 4\) oder \(\dfrac{4 \cdot 3}{10}\) schreibt. Allerdings ist bei allen drei Schreibweisen der "Malpunkt" zwingend erforderlich, da \(4 \dfrac{3}{10}\) als \(4 + \dfrac{3}{10}\) verstanden wird. Bei \(\dfrac{4 \cdot 3}{10}\) erklärt es sich eigentlich von selbst, warum der "Malpunkt" hier nicht einfach weggelassen werden darf ...
Bemerkung: Man kann Bruchstriche auch schräg schreiben. Das spart Platz und ist manchmal übersichtlicher.
Welche Arten von Brüchen gibt es?
Man unterscheidet folgende Arten von Brüchen:
Echte und unechte Brüche
Bei echten Brüchen ist der Betrag des Zählers kleiner als der Betrag des Nenners, d. h. der Betrag des gesamten Bruches ist kleiner als \(1\), z. B. \(\dfrac {3}{8}=0{,}375\) oder \(-\dfrac {4}{5}=-0{,}8\).
Bei unechten Brüchen ist der Betrag des Zählers größer als der Betrag des Nenners, d. h. der Betrag des gesamten Bruches ist größer als \(1\), z. B. \(\dfrac{11}{8}=1{,}375\) oder \(-\dfrac{17}{5}=-3{,}4\).
Gemischte Zahlen
Gemischte Zahlen bestehen aus einer ganzen Zahl und einem echten Bruch, z. B. \(\dfrac {13}{6}=\dfrac{12}{6}+\dfrac{1}{6}=2+ \dfrac{1}{6} = 2 \dfrac{1}{6}\) oder \(-\dfrac{13}{6}=-\left(2+\dfrac{1}{6}\right)\).
Ganz wichtig: Bitte beachten Sie, dass die ganze Zahl und der Bruch addiert werden, auch wenn das Pluszeichen weggelassen wird! Normalerweise werden in der Mathematik ausschließlich Malzeichen nicht geschrieben, wenn die Formel o. Ä. trotz des Weglassens eindeutig bleibt. Dies hier ist die große Ausnahme. Da das in vielen Fällen zu Verwirrung führt, sollte diese Schreibweise nur verwendet werden, wenn es dafür wichtige Gründe gibt! Und davon gibt es nicht sehr viele ...
Im Übrigen werden gemischte Zahlen eigentlich gar nicht benötigt. Echte und unechte Brüche reichen vollkommen aus, um alle Brüche abzubilden. Als Alternative gibt es auch noch die Dezimalzahlen. Statt einen unechten Bruch in eine gemischte Zahl umzuwandeln, ist es üblicherweise besser, ihn einfach so stehen zu lassen.
Gleichnamige und ungleichnamige Brüche
Brüche, die den gleichen Nenner haben, heißen gleichnamig. Der entsprechende Nenner heißt Hauptnenner der Brüche. Z. B. sind die Brüche \(\dfrac{1} {5}\) und \(\dfrac{4} {5}\) gleichnamig. Ihr Hauptnenner ist \(5\).
Brüche, die nicht den gleichen Nenner haben, heißen ungleichnamig, z. B. sind die Brüche \(\dfrac{2} {3}\) und \(\dfrac{2} {7}\) ungleichnamig.
Das "kleinste gemeinsame Vielfache" und der "größte gemeinsame Teiler"
Für das Erweitern und Kürzen, worum es ein Stück weiter unten gehen wird, sind die Konzepte vom kleinsten gemeinsamen Vielfachen (kgV) und vom größten gemeinsamen Teiler (ggT) zweier natürlicher Zahlen \(a\) und \(b\) (also \(a, b \in \mathbb {N}\)) nützlich:
Definition: Das kleinste gemeinsame Vielfache der Zahlen \(a\) und \(b\) ist die kleinste natürliche Zahl, die sowohl ein Vielfaches von \(a\) als auch ein Vielfaches von \(b\) ist, z. B. ist das kgV von \(3\) und \(5\) gleich \(15\).
Die Bestimmung des kgV hilft u. a., wenn zwei Brüche gleichnamig gemacht werden müssen, z. B. \(\dfrac{1}{6} + \dfrac{1}{8} = \dfrac{1 \cdot 4}{6 \cdot 4} + \dfrac{1 \cdot 3}{8 \cdot 3} = \dfrac{4}{24} + \dfrac{3}{24}\). Natürlich wäre auch \(48=6 \cdot 8\) ein Hauptnenner von \(\dfrac {1}{6}\) und \(\dfrac {1}{8}\). Allerdings wären dann die Zähler und Nenner jeweils doppelt so groß und üblicherweise rechnet es sich mit kleineren Zahlen leichter.
Definition: Der größte gemeinsame Teiler der Zahlen \(a\) und \(b\) ist die größte natürliche Zahl, durch die sich sowohl \(a\) als auch \(b\) ohne Rest teilen lässt, z. B. ist der ggT von \(7\) und \(21\) gleich \(7\).
Zahlen, deren ggT gleich \(1\) ist, heißen teilerfremd.
Rechenregeln für Brüche
Erweitern und Kürzen
Zwei Brüche werden erweitert, indem man Zähler und Nenner mit der gleichen Zahl multipliziert. Der Wert des Bruches ändert sich dabei nicht, z. B. \(\dfrac{3}{8}=\dfrac{3 \cdot 2}{8 \cdot 2}=\dfrac{6}{16}\).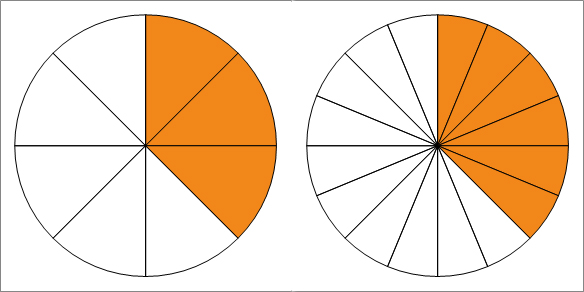
Zwei Brüche werden gekürzt, indem man Zähler und Nenner durch die gleiche Zahl dividiert. Der Wert des Bruches ändert sich dabei nicht, z. B. \(\dfrac{4}{12}=\dfrac{4 : 4} {12 : 4}=\dfrac{1}{3}\).
Wenn ein Bruch gekürzt werden soll, hilft die Bestimmung des ggT, z. B. ist \(4\) der ggT von \(4\) und \(12\).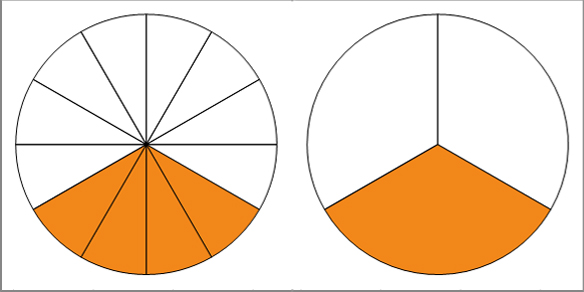
Es versteht sich (hoffentlich) von selbst, dass \(0\) keine geeignete Zahl zum Erweitern oder Kürzen ist, weil man ja nun mal durch \(0\) nicht teilen darf ...
Achtung: Aus Summen darf man nicht kürzen! Summen gehören ja schließlich zur Strichrechnung und das Kürzen zur Punktrechnung.
Noch ein paar Worte zum Kürzen aus Summen:
Auch wenn man es nicht auf den ersten Blick sieht, handelt es sich hierbei um eine Kombination von Addition/Subtraktion und Division, über die wir uns im Kapitel Rechengesetze schon Gedanken gemacht hatten. Wenn im Zähler oder Nenner eine Summe/Differenz steht, entsteht genau die Situation, in der wir auf die Rangfolge der Rechenoperationen achten müssen: Der Bruchstrich steht ja für eine Division und wirkt somit wie eine Klammer. Dazu kommt, dass auch das Kürzen eine Art von Dividieren ist. All das verträgt sich nicht mit der Strichrechnung ...
Käme man bei \(\frac{4+11}{4}\) auf die Idee, die \(4\) im Zähler mit der \(4\) im Nenner zu „kürzen“, erhielte man als Ergebnis \(11\).
Richtig ist aber \(\frac{4+11}{4} = \frac{15}{4} = 3{,}75\)
Addition und Subtraktion
 |
Zwei gleichnamige Brüche werden addiert, indem man die Zähler addiert und den Nenner beibehält, z. B. \(\dfrac{4}{10}+\dfrac{3}{10}=\dfrac{4+3}{10}=\dfrac{7}{10}\).
Zwei ungleichnamige Brüche werden addiert, indem man sie gleichnamig macht (z. B. durch Erweitern) und dann addiert, z. B. \(\dfrac{1}{2}+\dfrac{1}{3}= \dfrac{1 \cdot 3}{2 \cdot 3}+\dfrac{1 \cdot 2}{3 \cdot 2}=\dfrac{3}{6}+\dfrac{2}{6}=\dfrac{3+2}{6}=\dfrac{5}{6}\).
Zwei gleichnamige Brüche werden subtrahiert, indem man die Zähler subtrahiert und den Nenner beibehält, z. B. \(\dfrac{7}{10}-\dfrac{3}{10}=\dfrac{7-3}{10}=\dfrac{4}{10}\).
Zwei ungleichnamige Brüche werden subtrahiert, indem man sie gleichnamig macht (z. B. durch Erweitern) und dann subtrahiert, z. B. \(\dfrac{4} {5}-\dfrac{1}{15}=\dfrac{4 \cdot 3}{5 \cdot 3}-\dfrac{1}{15}=\dfrac{12}{15}-\dfrac{1}{15}=\dfrac{12-1}{15}= \dfrac{11}{15}\).
Ganz wichtig: Es gibt keine Rechenregel, die besagt, dass die Nenner irgendwie addiert bzw. subtrahiert werden müssen. Die Addition und Subtraktion von Brüchen funktioniert wirklich nur auf dem Weg, der hier vorgestellt wurde. Das gilt auch, wenn die Brüche Variablen enthalten, wie das in späteren Kapiteln der Fall sein wird. Dann mag es manchmal etwas umständlich sein, die Brüche gleichnamig zu machen - es muss aber sein!
Was passiert, wenn man die Brüche nicht gleichnamig macht, sehen sie an folgendem Vergleich:
Richtig ist: \(\frac{1}{2} +\frac{3}{4} = \frac{2}{4} + \frac{3}{4} = \frac{5}{4} > 1\)
Addiert man - fälschlicherweise - Zähler und Nenner von \(\frac{1}{2}\) und \(\frac{3}{4}\) separat, erhält man \(\frac{4}{6} < 1\). Da kann also was nicht stimmen…
Multiplikation und Division
Zwei Brüche werden multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert, z. B. \(\dfrac{1}{4} \cdot \dfrac{3}{7}=\dfrac{1 \cdot 3}{4 \cdot 7}=\dfrac{3} {28}\).
Zwei Brüche werden dividiert, indem man mit dem Kehrwert des zweiten Bruches multipliziert, z. B. \(\dfrac{1}{6} : \dfrac{2}{11}=\dfrac{1}{6} \cdot \dfrac{11}{2}=\dfrac{1 \cdot 11}{6 \cdot 2}=\dfrac{11}{12}\).
Bemerkung zur Multiplikation und Division: Nützlich ist, immer vor dem Multiplizieren zu überprüfen, ob die Brüche gegeneinander gekürzt werden können, da dadurch die Zahlen kleiner werden. Je früher in einer Rechnung gekürzt wird, desto handlicher bleibt die Aufgabe.
Beispiel: Multipliziert man bei \(\dfrac{33}{14} \cdot \dfrac{280}{15}\) einfach die beiden Zähler und die beiden Nenner, erhält man \(\dfrac{9{.}240}{210}\), wo nicht offensichtlich ist, durch welche Zahl gekürzt werden kann. Kürzt man vor dem Multiplizieren, sieht die Rechnung so aus: \(\dfrac{33}{14} \cdot \dfrac{280}{15} = \dfrac{11}{1} \cdot \dfrac{20}{5} = 11 \cdot 4 = 44\)
Vor dem Multiplizieren wurden hier die \(33\) (Zähler vom ersten Faktor) mit der \(15\) (Nenner vom zweiten Faktor) durch \(3\) sowie die \(14\) (Nenner vom ersten Faktor) mit der \(280\) (Zähler vom zweiten Faktor) durch \(14\) gekürzt.
Damit geht die gesamte Rechnung problemlos im Kopf ...
Bemerkung allgemein: Ist das Ergebnis einer Bruchrechnungsaufgabe ein Bruch, sollte dieser so weit wie möglich gekürzt werden. Abhängig von der Aufgabenstellung (z. B. wenn die Größenordnung von Bedeutung ist) kann es sinnvoll sein, das Ergebnis als Dezimalzahl oder in Ausnahmefällen als gemischte Zahl darzustellen. In anderen Situationen, z. B. beim Multiplizieren oder beim Abschätzen von Wurzeln, eignen sich Brüche wesentlich besser.
Im vorherigen Kapitel hieß es schon, dass ein Bruchstrich wie eine Klammer wirkt. Eine Klammer muss immer dann gesetzt werden, wenn der Bruchstrich durch : ersetzt wird bzw. wenn mehrere Brüche auf einem Bruchstrich zusammengefasst werden! Hier nun die versprochenen Beispiele:
- \(\dfrac{x+10}{3x-17}=(x+10) : (3x-17)\)
Diese Schreibweise ist z. B. für die Polynomdivision wichtig. - \(\dfrac{5}{4} \cdot \dfrac{x+10}{3x-17} = \dfrac{5\cdot (x+10)}{4\cdot (3x-17)} = \dfrac{5x+50}{12x-68}\)
Hier müssen im zweiten Bruch Klammern gesetzt werden, weil die Regel für die Multiplikation von Brüchen ja lautet "Zähler mal Zähler" und "Nenner mal Nenner". Ohne Klammern hätte man \(5\cdot x+10\) und \(4\cdot 3x -17\) , würde also nur einen Teil vom zweiten Zähler/Nenner mit dem Zähler/Nenner vom ersten Bruch multiplizieren. - \(\dfrac{5-8x}{7x+4} \cdot \dfrac{x+10}{3x-17} = \dfrac{(5-8x) \cdot (x+10)}{(7x+4) \cdot (3x-17)} = \dfrac{5x+50-8x\cdot x-80x}{21x\cdot x-119x+12x-68}\)
Hier ist es ebenso. Zusätzlich gelten natürlich auch bei Brüchen die "ganz normalen" Rechengesetze, wie Distributiv-, Kommutativ- und Assoziativgesetz. Anders gesagt: Ausmultiplizieren funktioniert im Zähler und Nenner genauso wie ohne Bruch drumherum ...
Zum Abschluss noch ein Beispiel, nur mit Zahlen, damit leichter zu sehen ist, warum das mit den Klammern auch wirklich wichtig ist:
| Betrachten wir die Aufgabe | \(\dfrac{2}{3}\cdot\dfrac{1+1}{4+5}\) | \(=\) | \(\dfrac{2\cdot (1+1)}{3\cdot (4+5)}\) | \(=\) | \(\dfrac{2\cdot 2}{3\cdot 9}\) | \(=\) | \(\dfrac{4}{27}\) | \(=\) | \(0{,}\overline{148}\) | Das ist offensichtlich nicht das Gleiche! | |
| Ohne Klammern stünde dort | \(\dfrac{2\cdot 1+1}{3\cdot 4+5}\) | \(=\) | \(\dfrac{2+1}{12+5}\) | \(=\) | \(\dfrac{3}{17}\) | \(\approx\) | \(0{,}17647\) |
Übersicht:
Aufgaben
Alle diese Aufgaben sollten Sie ohne Taschenrechner berechnen. Sinn der Übung ist ja nicht, dass Sie Ihren Taschenrechner bedienen lernen, sondern dass Sie den Umgang mit Brüchen trainieren. Spätestens in Kapitel 5, in dem Variablen ins Spiel kommen, hilft Ihnen der Taschenrechner ohnehin nur noch eingeschränkt weiter ... Wenn man dann den Umgang mit Brüchen nie geübt hat, gehen auch Ableitungen und Integrale leicht schief - selbst wenn man die wesentlich komplizierteren Ableitungs- und Integrationsregeln eigentlich kann.
1. Aufgabe
Erweitern Sie die folgenden Brüche mit der jeweils angegebenen Zahl!
| 1) \(\dfrac {4}{5}\) mit \(3\) |
11) \(\dfrac {29}{30}\) mit \(4\) |
|
| 2) \(\dfrac{1}{10}\) mit \(12\) |
12) \(\dfrac{654}{125}\) mit \(3\) |
|
| 3) \(\dfrac{7}{12}\) mit \(5\) |
13) \(\dfrac{70}{93}\) mit \(80\) |
|
| 4) \(\dfrac{583}{15}\) mit \(10\) |
14) \(\dfrac{12}{35}\) mit \(6\) |
|
| 5) \(\dfrac {2}{3}\) mit \(21\) |
15) \(\dfrac {576}{688}\) mit \(1.000\) |
|
| 6) \(\dfrac{123}{456}\) mit \(100\) |
16) \(\dfrac{334}{777}\) mit \(2\) |
|
| 7) \(\dfrac{5}{6}\) mit \(4\) |
17) \(\dfrac{6}{7}\) mit \(13\) |
|
| 8) \(\dfrac{3}{8}\) mit \(11\) |
18) \(\dfrac{70}{3}\) mit \(5\) |
|
| 9) \(\dfrac{11}{7}\) mit \(9\) |
19) \(\dfrac{5}{8}\) mit \(9\) |
|
| 10) \(\dfrac{211}{30}\) mit \(25\) |
20) \(\dfrac{130}{621}\) mit \(20\) |
2. Aufgabe
Erweitern Sie die folgenden Brüche so, dass sie gleichnamig werden.
| 1) \(\dfrac{10}{13}\) und \(\dfrac {2}{3}\) |
11) \(\dfrac {1}{2}\) und \(\dfrac{1}{20}\) und \(\dfrac{3}{10}\) |
|
| 2) \(\dfrac {8}{9}\) und \(\dfrac{4}{15}\) |
12) \(\dfrac {1}{3}\) und \(\dfrac{7}{20}\) und \(\dfrac{2}{11}\) |
|
| 3) \(\dfrac {1}{8}\) und \(\dfrac {5}{6}\) |
13) \(\dfrac {7}{4}\) und \(\dfrac{1}{20}\) und \(\dfrac{132}{5}\) |
|
| 4) \(\dfrac{99}{12}\) und \(\dfrac{5}{18}\) |
14) \(\dfrac {3}{70}\) und \(\dfrac{201}{30}\) und \(\dfrac{1}{14}\) |
|
| 5) \(\dfrac{11}{20}\) und \(\dfrac{2}{19}\) |
15) \(\dfrac {5}{21}\) und \(\dfrac {1}{12}\) und \(\dfrac{4} {3}\) und \(\dfrac{2}{21}\) |
|
| 6) \(\dfrac{20}{7}\) und \(\dfrac{7}{50}\) |
16) \(\dfrac {3}{4}\) und \(\dfrac {1}{8}\) und \(\dfrac{13} {16}\) und \(\dfrac{5}{24}\) |
|
| 7) \(\dfrac{17}{3}\) und \(\dfrac{10}{9}\) |
17) \(\dfrac {3}{5}\) und \(\dfrac {20}{7}\) und \(\dfrac{13} {2}\) und \(\dfrac{54}{70}\) |
|
| 8) \(\dfrac{3}{11}\) und \(\dfrac{1}{6}\) |
18) \(\dfrac {19}{2}\) und \(\dfrac {13}{6}\) und \(\dfrac{37} {120}\) und \(\dfrac{91}{180}\) |
|
| 9) \(\dfrac{32}{27}\) und \(\dfrac{3}{2}\) |
19) \(\dfrac {1}{7}\) und \(\dfrac{8} {9}\) und \(\dfrac{33} {14}\) und \(\dfrac{10} {63}\) und \(\dfrac{25} {24}\) |
|
| 10) \(\dfrac{3}{100}\) und \(\dfrac{7}{4}\) |
20) \(\dfrac {1}{2}\) und \(\dfrac{1} {3}\) und \(\dfrac{1} {4}\) und \(\dfrac{1} {5}\) und \(\dfrac{1} {6}\) und \(\dfrac{1} {15}\) und \(\dfrac{1} {36}\) |
3. Aufgabe
Kürzen Sie die folgenden Brüche so weit wie möglich!
| 1) \(\dfrac{10}{18}\) |
11) \(\dfrac{121}{22}\) |
|
| 2) \(\dfrac{51}{17}\) |
12) \(\dfrac{91}{70}\) |
|
| 3) \(\dfrac{38}{171}\) |
13) \(\dfrac{90}{810}\) |
|
| 4) \(\dfrac{30}{205}\) |
14) \(\dfrac{96}{48}\) |
|
| 5) \(\dfrac{38}{4}\) |
15) \(\dfrac{131}{3}\) |
|
| 6) \(\dfrac{124.000}{987.000}\) |
16) \(\dfrac{2.500}{5.000}\) |
|
| 7) \(\dfrac{21}{49}\) |
17) \(\dfrac{110}{1.320}\) |
|
| 8) \(\dfrac{39}{169}\) |
18) \(\dfrac{42}{7}\) |
|
| 9) \(\dfrac{28}{42}\) |
19) \(\dfrac{69}{6}\) |
|
| 10) \(\dfrac{23}{30}\) |
20) \(\dfrac{120}{18}\) |
4. Aufgabe
Wandeln Sie die folgenden unechten Brüche in gemischte Zahlen um und umgekehrt. Kürzen Sie die entstehenden Brüche, wenn möglich.
| 1) \(\dfrac{67}{6}\) |
11) \(2\dfrac{1}{9}\) |
|
| 2) \(\dfrac{25}{23}\) |
12) \(1\dfrac{13}{14}\) |
|
| 3) \(\dfrac{94}{24}\) |
13) \(8\dfrac{4}{7}\) |
|
| 4) \(\dfrac{119}{17}\) |
14) \(10\dfrac{14}{15}\) |
|
| 5) \(\dfrac{235}{50}\) |
15) \(5\dfrac{20}{33}\) |
|
| 6) \(\dfrac{95}{3}\) |
16) \(12\dfrac{3}{4}\) |
|
| 7) \(\dfrac{123}{11}\) |
17) \(3\dfrac{14}{27}\) |
|
| 8) \(\dfrac{155}{12}\) |
18) \(19\dfrac{1}{8}\) |
|
| 9) \(\dfrac{41}{7}\) |
19) \(63\dfrac{7}{9}\) |
|
| 10) \(\dfrac{80}{9}\) |
20) \(32\dfrac{11}{13}\) |
5. Aufgabe
Wandeln Sie folgende Brüche in Dezimalzahlen um (wenn nötig, gerundet auf 4 Stellen nach dem Komma) und umgekehrt.
| 1) \(\dfrac{7}{12}\) |
11) \(0{,}24\) |
|
| 2) \(\dfrac{18}{5}\) |
12) \(2{,}\overline{6}\) |
|
| 3) \(\dfrac{61}{650}\) |
13) \(0{,}67\) |
|
| 4) \(\dfrac{18}{18}\) |
14) \(6{,}25\) |
|
| 5) \(\dfrac{23}{16}\) |
15) \(0{,}\overline{83}\) |
|
| 6) \(\dfrac{2}{99}\) |
16) \(3{,}008\) |
|
| 7) \(\dfrac{120}{10}\) |
17) \(0{,}5058\) |
|
| 8) \(\dfrac{63}{85}\) |
18) \(5\) |
|
| 9) \(\dfrac{16}{25}\) |
19) \(6{,}625\) |
|
| 10) \(\dfrac{1}{130}\) |
20) \(0{,}025\) |
6. Aufgabe
Berechnen Sie folgende Aufgaben.
| 1) \(\dfrac{3}{4} \, + \, \dfrac{3}{2} \) |
11) \( 34 \cdot \dfrac{1}{2} \) |
|
| 2) \(1\dfrac{5}{6} \, + \, 2\dfrac{7}{8} \) |
12) \(2\dfrac{1}{4} \, \cdot \, \dfrac{2} {7}\) |
|
| 3) \(\dfrac{3}{2} \, + \, 12\) |
13) \( \dfrac{3}{8} \, : \, \dfrac{5}{4} \) |
|
| 4) \( \dfrac{9}{11} + \dfrac{3}{4} \) |
14) \( \dfrac{5}{6} \, : \, \dfrac{25}{12} \) |
|
| 5) \( \dfrac{1}{7} \, - \, \dfrac{3}{5} \) |
15) \( \dfrac{8}{9} : \dfrac{4}{27} \) |
|
| 6) \( 11 - \dfrac{13}{3} \) |
16) \( 4\dfrac{2}{5} \, : \, 3\dfrac{1}{10} \) |
|
| 7) \( 4\dfrac{2}{9} \, - \, 1\dfrac{1}{3} \) |
17) \( 4-\dfrac{2}{3} \, \cdot \, \dfrac{5}{8} \) |
|
| 8) \(-\dfrac{20}{7}-\dfrac{7}{10} \) |
18) \( \dfrac{1}{2} \, + \, 5 \, : \, \dfrac{10}{13} \, + \, 2\dfrac{1}{8} \) |
|
| 9) \( \dfrac{42}{5} \cdot \dfrac{10}{63} \) |
19) \( \dfrac{13}{7} \, : \, \left( -\dfrac{26}{21} \right) \, \cdot \, \dfrac{8}{27} \) |
|
| 10) \( \dfrac{7}{9} \cdot 6\) |
20) \( -\dfrac{3}{2} \, + \, \dfrac{15}{4} \, \cdot \, \left( -\dfrac{16}{5} \right) \, - \, \dfrac{9}{6} \, : \, \left(-3\right) \) |
7. Aufgabe
| 1) \(\genfrac{}{}{1pt}{0}{\frac{3}{2}}{\frac{7}{3}} \) |
11) \(\genfrac{}{}{1pt}{0}{-\frac{21}{8}}{-\frac{12}{5}}\) |
|
| 2) \(\genfrac{}{}{1pt}{0}{\frac{-5}{-3}}{-\frac{25}{4}}\) |
12) \(\genfrac{}{}{1pt}{0}{-34}{\frac{-43}{-12}}\) | |
| 3) \(\genfrac{}{}{1pt}{0}{-15}{\frac{11}{-30}}\) |
13) \(\genfrac{}{}{1pt}{0}{\frac{-5}{72}}{\frac{-40}{11}} \) | |
| 4) \(\genfrac{}{}{1pt}{0}{\frac{8}{12}}{5}\) |
14) \(\genfrac{}{}{1pt}{0}{\frac{5}{4}}{-\frac{21}{52}}\) | |
| 5) \(\genfrac{}{}{1pt}{0}{\frac{38}{-3}}{\frac{19}{4}}\) |
15) \(\genfrac{}{}{1pt}{0}{\frac{19}{15}}{\frac{-7}{102}}\) | |
| 6) \(\genfrac{}{}{1pt}{0}{\frac{27}{16}}{\frac{3}{11}}\) |
16) \(\genfrac{}{}{1pt}{0}{\frac{-33}{16}}{-\frac{99}{14}}\) | |
| 7) \(\genfrac{}{}{1pt}{0}{113}{\frac{17}{2}}\) | 17) \(-\genfrac{}{}{1pt}{0}{-\frac{121}{17}}{\frac{77}{170}}\) | |
| 8) \(\genfrac{}{}{1pt}{0}{\frac{-42}{5}}{102}\) | 18) \(\genfrac{}{}{1pt}{0}{\frac{142}{27}}{\frac{71}{72}}\) | |
| 9) \(\genfrac{}{}{1pt}{0}{-\frac{1}{9}}{\frac{1}{81}}\) | 19) \(\genfrac{}{}{1pt}{0}{\frac{2}{15}}{\frac{-46}{-65}}\) | |
| 10) \(\genfrac{}{}{1pt}{0}{\frac{14}{23}}{-6}\) | 20) \(\genfrac{}{}{1pt}{0}{-\frac{25}{256}}{-\frac{225}{32}}\) |
8. Aufgabe
Berechnen Sie so schnell wie möglich und ohne Hilfsmittel!
Wie viel ist die Hälfte von zwei Drittel von drei Viertel von vier Fünftel von fünf Sechstel von sechs Siebtel von sieben Achtel von acht Neuntel von neun Zehntel von \(10\)?
9. Aufgabe
Gesucht ist für jedes Sternchen eine Ziffer (also \(0\), \(1\), \(2\), ... \(9\)) oder - falls sich keine Ziffer finden lässt - eine möglichst kleine natürliche Zahl, sodass die Rechnungen stimmen. Verschiedene Sternchen innerhalb einer Aufgabe können dabei durchaus verschiedene Ziffern / Zahlen bedeuten. Begründen Sie Ihre Ergebnisse!
Bemerkung: Diese Aufgaben sind ein bisschen tricky, führen aber gleichzeitig sehr schön in mathematische Denkweisen und Argumentationen ein - und benötigen dabei nicht mehr als die Grundrechenarten und Bruchrechnung.
1) \(\dfrac{*}{11}-\dfrac{28}{*} \, = \, 0\)
2) \(\dfrac{*}{3}\cdot \dfrac{*}{8} \, = \, \dfrac{35}{*}\)
3) \(\dfrac{5}{*}+\dfrac{*}{5} \, = \, 4\dfrac{9}{10}\)
4) \(\dfrac{1}{5}-\dfrac{*}{9} \, = \, -\dfrac{1}{*}\)
5) \(\dfrac{*}{4}+\dfrac{13}{*} \, = \, \dfrac{0}{*}\)
6) \(\dfrac{5}{*1} : \dfrac{2}{*} \, = \, \dfrac{5}{2*}\)
Übersicht:
- Lösung zur 1. Aufgabe
- Lösung zur 2. Aufgabe
- Lösung zur 3. Aufgabe
- Lösung zur 4. Aufgabe
- Lösung zur 5. Aufgabe
- Lösung zur 6. Aufgabe
- Lösung zur 7. Aufgabe
- Lösung zur 8. Aufgabe
- Lösung zur 9. Aufgabe
Lösungen
1. Aufgabe
| 1) \(\dfrac{4}{5}=\dfrac{4 \cdot 3}{5 \cdot 3}=\dfrac{12}{15}\) |
11) \(\dfrac{29}{30}=\dfrac{29 \cdot 4}{30 \cdot 4}=\dfrac{116}{120}\) |
|
| 2) \(\dfrac{1}{10}=\dfrac{1 \cdot 12}{10 \cdot 12}=\dfrac{12}{120}\) |
12) \(\dfrac{654}{125}=\dfrac{654 \cdot 3}{125 \cdot 3}=\dfrac{1.962}{375}\) |
|
| 3) \(\dfrac{7}{12}=\dfrac{7 \cdot 5}{12 \cdot 5}=\dfrac{35}{60}\) |
13) \(\dfrac{70}{93}=\dfrac{70 \cdot 80}{93 \cdot 80}=\dfrac{5.600}{7.440}\) |
|
| 4) \(\dfrac{583}{15}=\dfrac{583 \cdot 10}{15 \cdot 10}=\dfrac{5.830}{150}\) |
14) \(\dfrac{12}{35}=\dfrac{12 \cdot 6}{35 \cdot 6}=\dfrac{72}{210}\) |
|
| 5) \(\dfrac{2}{3}=\dfrac{2 \cdot 21}{3 \cdot 21}=\dfrac{42}{63}\) |
15) \(\dfrac{576}{688}=\dfrac{576 \cdot 1.000}{688 \cdot 1.000}=\dfrac{576.000}{688.000}\) |
|
| 6) \(\dfrac{123}{456}=\dfrac{123 \cdot 100}{456 \cdot 100}=\dfrac{12.300}{45.600}\) |
16) \(\dfrac{334}{777}=\dfrac{334 \cdot 2}{777 \cdot 2}=\dfrac{668}{1.554}\) |
|
| 7) \(\dfrac{5}{6}=\dfrac{5 \cdot 4}{6 \cdot 4}=\dfrac{20}{24}\) |
17) \(\dfrac{6}{7}=\dfrac{6\cdot 13}{7 \cdot 13}=\dfrac{78}{91}\) |
|
| 8) \(\dfrac{3}{8}=\dfrac{3 \cdot 11}{8 \cdot 11}=\dfrac{33}{88}\) |
18) \(\dfrac{70}{3}=\dfrac{70\cdot 5}{3\cdot 5}=\dfrac{350}{15}\) |
|
| 9) \(\dfrac{11}{7}=\dfrac{11 \cdot 9}{7 \cdot 9}=\dfrac{99}{63}\) |
19) \(\dfrac{5}{8}=\dfrac{5\cdot 9}{8\cdot 9}=\dfrac{45}{72}\) |
|
| 10) \(\dfrac{211}{30}=\dfrac{211 \cdot 25}{30 \cdot 25}=\dfrac{5275}{750}\) |
20) \(\dfrac{130}{621}=\dfrac{130\cdot 20}{621\cdot 20}=\dfrac{2.600}{12.420}\) |
2. Aufgabe
1) \(\dfrac{10}{13}=\dfrac{10 \cdot 3}{13 \cdot 3}=\dfrac{30}{39} \) und \(\dfrac{2}{3}=\dfrac{2 \cdot 13}{3 \cdot 13}= \dfrac{26}{39}\)
2) \(\dfrac{8}{9}=\dfrac{8 \cdot 5}{9 \cdot 5}=\dfrac{40}{45}\) und \(\dfrac{4}{15}= \dfrac{4 \cdot 3}{15 \cdot 3}=\dfrac{12}{45}\)
3) \(\dfrac{1}{8}=\dfrac{1 \cdot 3}{8 \cdot 3}=\dfrac{3} {24}\) und \(\dfrac{5}{6}=\dfrac{5 \cdot 4}{6 \cdot 4}=\dfrac{20}{24}\)
4) \(\dfrac{99}{12}=\dfrac{99 \cdot 3}{12 \cdot 3}=\dfrac{297}{36}\) und \(\dfrac{5}{18}=\dfrac{5 \cdot 2}{18 \cdot 2}=\dfrac{10}{36}\)
5) \(\dfrac{11}{20}=\dfrac{11 \cdot 19}{20 \cdot 19}=\dfrac{209}{380}\) und \(\dfrac{2}{19}=\dfrac{2 \cdot 20}{19 \cdot 20}=\dfrac{40}{380}\)
6) \(\dfrac{20}{7}=\dfrac{20 \cdot 50}{7 \cdot 50}=\dfrac{1000}{350} \) und \(\dfrac{7}{50}=\dfrac{7 \cdot 7}{50 \cdot 7}= \dfrac{49}{350}\)
7) \(\dfrac {17}{3}=\dfrac{17 \cdot 3}{3 \cdot 3}=\dfrac{51}{9}\) und \(\dfrac{10}{9}\)
8) \(\dfrac {3}{11}=\dfrac{3 \cdot 6}{11 \cdot 6}=\dfrac{18}{66}\) und \(\dfrac {1}{6}=\dfrac{1 \cdot 11}{6 \cdot 11}=\dfrac{11}{66}\)
9) \(\dfrac {32}{27}=\dfrac{32 \cdot 2}{27 \cdot 2}=\dfrac{64}{54}\) und \(\dfrac {3}{2}=\dfrac{3 \cdot 27}{2 \cdot 27}=\dfrac{81}{54}\)
10) \(\dfrac{3}{100}\) und \(\dfrac{7}{4}=\dfrac{7 \cdot 25}{4 \cdot 25}=\dfrac{175}{100}\)
11) \(\dfrac{1}{2}=\dfrac{1 \cdot 10}{2 \cdot 10}=\dfrac{10}{20}\) und \(\dfrac{1} {20}\) und \(\dfrac{3}{10}=\dfrac{3 \cdot 2}{10 \cdot 2}=\dfrac{6}{20}\)
12) \(\dfrac {1}{3}=\dfrac{1 \cdot 220}{3 \cdot 220}=\dfrac{220}{660}\) und \(\dfrac{7}{20}=\dfrac{7 \cdot 33}{20 \cdot 33}=\dfrac{231}{660}\) und \(\dfrac {2}{11}=\dfrac{2 \cdot 60}{11 \cdot 60}=\dfrac{120}{660}\)
13) \(\dfrac {7}{4}=\dfrac{7 \cdot 5}{4 \cdot 5}=\dfrac{35}{20}\) und \(\dfrac{1}{20}\) und \(\dfrac {132}{5}=\dfrac{132 \cdot 4}{5 \cdot 4}=\dfrac{528}{20}\)
14) \(\dfrac {3}{70}=\dfrac{3 \cdot 6}{70 \cdot 6}=\dfrac{18}{420}\) und \(\dfrac{201}{30}=\dfrac{201 \cdot 14}{30 \cdot 14}=\dfrac{2814}{420}\) und \(\dfrac {1}{14}=\dfrac{1 \cdot 30}{14 \cdot 30}=\dfrac{30}{420}\)
15) \(\dfrac {5}{21}=\dfrac{5 \cdot 4}{21 \cdot 4}=\dfrac{20}{84}\) und \(\dfrac {1}{12}=\dfrac{1 \cdot 7}{12 \cdot 7}=\dfrac{7}{84}\) und \(\dfrac {4}{3}=\dfrac{4 \cdot 28}{3 \cdot 28}=\dfrac{112}{84}\) und \(\dfrac {2}{21}=\dfrac{2 \cdot 4}{21 \cdot 4}=\dfrac{8}{84}\)
16) \(\dfrac {3}{4}=\dfrac{3 \cdot 12}{4 \cdot 12}=\dfrac{36}{48}\) und \(\dfrac {1}{8}=\dfrac{1 \cdot 6}{8 \cdot 6}=\dfrac{6}{48}\) und \(\dfrac {13}{16}=\dfrac{13 \cdot 3}{16 \cdot 3}=\dfrac{39}{48}\) und \(\dfrac {5}{24}=\dfrac{5 \cdot 2}{24 \cdot 2}=\dfrac{10}{48}\)
17) \(\dfrac {3}{5}=\dfrac{3 \cdot 14}{5 \cdot 14}=\dfrac{42}{70}\) und \(\dfrac {20}{7}=\dfrac{20 \cdot 10}{7 \cdot 10}=\dfrac{200}{70}\) und \(\dfrac {13}{2}=\dfrac{13 \cdot 35}{2 \cdot 35}=\dfrac{455}{70}\) und \(\dfrac {54}{70}\)
18) \(\dfrac {19}{2}=\dfrac{19 \cdot 180}{2 \cdot 180}=\dfrac{3420}{360}\) und \(\dfrac {13}{6}=\dfrac{13 \cdot 60}{6 \cdot 60}=\dfrac{780}{360}\) und \(\dfrac {37}{120}=\dfrac{37 \cdot 3}{120 \cdot 3}=\dfrac{111}{360}\) und \(\dfrac {91}{180}=\dfrac{91 \cdot 2}{180 \cdot 2}=\dfrac{182}{360}\)
19) \(\dfrac {1}{7}=\dfrac{1 \cdot 72}{7 \cdot 72}=\dfrac{72}{504}\) und \(\dfrac{8}{9}=\dfrac{8 \cdot 56}{9 \cdot 56}=\dfrac{448}{504}\) und \(\dfrac{33} {14}=\dfrac{33 \cdot 36}{14 \cdot 36}=\dfrac{1188}{504}\) und \(\dfrac{10}{63}=\dfrac{10 \cdot 8}{63 \cdot 8}=\dfrac{80}{504}\) und \(\dfrac {25}{24}=\dfrac{25 \cdot 21}{24 \cdot 21}=\dfrac{525}{504}\)
20) \(\dfrac {1}{2}=\dfrac{1 \cdot 90}{2 \cdot 90}=\dfrac{90}{180}\) und \(\dfrac{1} {3}=\dfrac{1 \cdot 60}{3 \cdot 60}=\dfrac{60}{180}\) und \(\dfrac{1} {4}=\dfrac{1 \cdot 45}{4 \cdot 45}=\dfrac{45}{180}\) und \(\dfrac{1} {5}=\dfrac{1 \cdot 36}{5 \cdot 36}=\dfrac{36}{180}\) und \(\dfrac {1} {6}=\dfrac{1 \cdot 30}{6 \cdot 30}=\dfrac{30}{180}\) und \(\dfrac{1} {15}=\dfrac{1 \cdot 12}{15 \cdot 12}=\dfrac{12} {180}\) und \(\dfrac{1} {36}=\dfrac{1 \cdot 5}{36 \cdot 5}=\dfrac{5}{180}\)
3. Aufgabe
| 1) \(\dfrac{10}{18}=\dfrac{10 : 2}{18 : 2}=\dfrac{5}{9}\) |
11) \(\dfrac{121}{22}=\dfrac{121 : 11}{22 : 11}=\dfrac{11}{2}\) |
|
| 2) \(\dfrac{51}{17}=\dfrac{51 : 17}{17 : 17}=3\) |
12) \(\dfrac{91}{70}=\dfrac{91 : 7}{70 : 7}=\dfrac{13}{10}\) |
|
| 3) \(\dfrac{38}{171}=\dfrac{38 : 19}{171 : 19}=\dfrac{2}{9}\) |
13) \(\dfrac{90}{810}=\dfrac{90 : 90}{810 : 90}=\dfrac{1}{9}\) |
|
| 4) \(\dfrac{30}{205}=\dfrac{30 : 5}{205 : 5}=\dfrac{6}{41}\) |
14) \(\dfrac{96}{48}=\dfrac{96 : 12}{48 : 12}=\dfrac{8}{4} = 2\) |
|
| 5) \(\dfrac{38}{4}= \dfrac{38 : 2}{4 : 2}=\dfrac{19}{2}\) |
15) \(\dfrac{131}{3}=\dfrac{131}{3}\) |
|
| 6) \(\dfrac{124.000}{987.000}= \dfrac{124.000 : 1.000}{987.000 : 1.000}=\dfrac{124}{987}\) |
16) \(\dfrac{2.500}{5.000}=\dfrac{2.500 : 100}{5.000 : 100}=\dfrac{25 : 25}{50 : 25}=\dfrac{1}{2}\) |
|
| 7) \(\dfrac{21}{49}= \dfrac{21 : 7}{49 : 7}=\dfrac{3}{7}\) |
17) \(\dfrac{110}{1.320}=\dfrac{110 : 110}{1.320 : 110}=\dfrac{1}{12}\) |
|
| 8) \(\dfrac{39}{169}= \dfrac{39 : 13}{169 : 13}=\dfrac{3}{13}\) |
18) \(\dfrac{42}{7}=\dfrac{42 : 7}{7 : 7}=\dfrac{6}{1}=6\) |
|
| 9) \(\dfrac{28}{42}= \dfrac{28 : 14}{42 : 14}=\dfrac{2}{3}\) |
19) \(\dfrac{69}{6}=\dfrac{69 : 3}{6 : 3}=\dfrac{23}{2}\) |
|
| 10) \(\dfrac{23}{30}\) Bemerkung: \(23\) und \(30\) enthalten keine gemeinsamen Teiler. Also kann man diesen Bruch nicht kürzen. |
20) \(\dfrac{120}{18}=\dfrac{120 : 6}{18 : 6}=\dfrac{20}{3}\) |
4. Aufgabe
| 1) \(\dfrac{67}{6}=\dfrac{66}{6}+\dfrac{1}{6}=11\dfrac{1}{6}\) |
11) \(2\dfrac{1}{9}=\dfrac{2\cdot 9}{9}+\dfrac{1}{9}=\dfrac{18}{9}+\dfrac{1}{9}=\dfrac{19}{9}\) |
|
| 2) \(\dfrac{25}{23}=\dfrac{23}{23}+\dfrac{2} {23}=1\dfrac{2}{23}\) |
12) \(1\dfrac{13}{14}=\dfrac{1\cdot 14} {14}+\dfrac{13}{14}=\dfrac{14} {14}+\dfrac{13}{14}=\dfrac{27}{14}\) |
|
| 3) \(\dfrac{94}{24}=\dfrac{72}{24}+\dfrac{22}{24}=3\dfrac{22}{24}=3\dfrac{11}{12}\) |
13) \(8\dfrac{4}{7}=\dfrac{8\cdot 7}{7}+\dfrac{4}{7}=\dfrac{56}{7}+\dfrac{4}{7}=\dfrac{60}{7}\) |
|
| 4) \(\dfrac{119}{17}=7\) |
14) \(10\dfrac{14}{15}=\dfrac{10\cdot 15}{15}+\dfrac{14}{15}=\dfrac{150}{15}+\dfrac{14}{15}=\dfrac{164}{15}\) |
|
| 5) \(\dfrac{235}{50}=\dfrac{200}{50}+\dfrac{35}{50}=4\dfrac{35}{50}=4\dfrac{7}{10}\) |
15) \(5\dfrac{20}{33}=\dfrac {5\cdot 33}{33}+\dfrac{20}{33}=\dfrac {165}{33}+\dfrac{20}{33}=\dfrac{185}{33}\) |
|
| 6) \(\dfrac{95}{3}=\dfrac{93}{3}+\dfrac{2}{3}=31\dfrac{2}{3}\) |
16) \(12\dfrac{3}{4}=\dfrac{12 \cdot 4}{4}+\dfrac{3}{4}=\dfrac{48}{4}+\dfrac{3}{4}=\dfrac{51}{4}\) |
|
| 7) \(\dfrac{123}{11}=\dfrac{121}{11}+\dfrac{2}{11}=11\dfrac{2}{11}\) |
17) \(3\dfrac{14}{27}=\dfrac{3 \cdot 27}{27}+\dfrac{14}{27}=\dfrac{81}{27}+\dfrac{14}{27}=\dfrac{95}{27}\) |
|
| 8) \(\dfrac{155}{12}=\dfrac{144}{12}+\dfrac{11}{12}=12\dfrac{11}{12}\) |
18) \(19\dfrac{1}{8}=\dfrac{19 \cdot 8}{8}+\dfrac{1}{8}=\dfrac{152}{8}+\dfrac{1}{8}=\dfrac{153}{8}\) |
|
| 9) \(\dfrac{41}{7}=\dfrac{35}{7}+\dfrac{6}{7}=5\dfrac{6}{7}\) |
19) \(63\dfrac{7}{9}=\dfrac{63 \cdot 9}{9}+\dfrac{7}{9}=\dfrac{567}{9}+\dfrac{7}{9}=\dfrac{574}{9}\) |
|
| 10) \(\dfrac{80}{9}=\dfrac{72}{9}+\dfrac{8}{9}=8\dfrac{8}{9}\) |
20) \(32\dfrac{11}{13}=\dfrac{32 \cdot 13}{13}+\dfrac{11}{13}=\dfrac{416}{13}+\dfrac{11}{13}=\dfrac{427}{13}\) |
5. Aufgabe
| 1) \(\dfrac{7}{12}=7:12\approx0{,}5833\) | 11) \(0{,}24=\dfrac{24}{100}=\dfrac{6}{25}\) |
|
| 2) \(\dfrac{18}{5}=18:5=3{,}6\) |
12) \(2{,}\overline{6}=2+\dfrac{6}{9}=\dfrac{2\cdot9}{9}+\dfrac{6}{9}=\dfrac{24}{9}=\dfrac{8}{3}\) |
|
| 3) \(\dfrac{61}{650}=61:650\approx0{,}0938\) |
13) \(0{,}67=\dfrac{67}{100}\) |
|
| 4) \(\dfrac{18}{18}=18:18=1\) |
14) \(6{,}25=\dfrac{25}{4}\) |
|
| 5) \(\dfrac{23}{16}=23:16=1{,}4375\) |
15) \(0{,}\overline{83}=\dfrac{83}{99}\) |
|
| 6) \(\dfrac{2}{99}=2:99\approx0{,}0202\) |
16) \(3{,}008=\dfrac{376}{125}\) |
|
| 7) \(\dfrac{120}{10}=120:10=12\) |
17) \(0{,}5058=\dfrac{2529}{5000}\) |
|
| 8) \(\dfrac{63}{85}=63:85\approx0{,}7412\) |
18) \(5=\dfrac{5}{1}\) |
|
| 9) \(\dfrac{16}{25}=16:25=0{,}64\) |
19) \(6{,}625=\dfrac{53}{8}\) |
|
| 10) \(\dfrac{1}{130}=1:130\approx0{,}0077\) |
20) \(0{,}025=\dfrac{1}{40}\) |
6. Aufgabe
Wichtig: Bei allen Multiplikations- und Divisionsaufgaben, in denen gemischte Zahlen enthalten sind, muss die gemischte Zahl vor dem Multiplizieren bzw. Dividieren in einen unechten Bruch umgewandelt werden, sonst kommen anschließend Punkt- und Strichrechnung durcheinander ...
Zur Wiederholung: Dies ist die einzige Stelle in der Mathematik, bei der nicht ein Malzeichen, sondern ein Pluszeichen weggelassen wird. Steht in einer Aufgabe z. B. die gemischte Zahl \(1\dfrac{1}{2}\), ist damit die Summe \(1+\dfrac{1} {2}\) gemeint. Diese Schreibweise verkompliziert Rechnungen also eher bzw. macht sie fehleranfälliger. Sie wird in diesem Lernmodul auch nur eingeführt, weil z. B. einige Taschenrechner sie verwenden und es deswegen nötig ist zu verstehen, wie sie gelesen werden muss.
1) \( \dfrac{3}{4} \, + \, \dfrac{3}{2} \, = \, \dfrac{3}{4} \, + \, \dfrac{3 \cdot 2}{2 \cdot 2} \, = \, \dfrac{3}{4} \, + \, \dfrac{6}{4} \, = \, \dfrac{9}{4} \, = \, 2\dfrac{1}{4} \)
2) \({ 1\dfrac{5}{6}+2\dfrac{7}{8}=\dfrac{6}{6}+\dfrac{5}{6}+\dfrac{16}{8}+\dfrac{7}{8}=\dfrac{11}{6}+\dfrac{23}{8}=\dfrac{11 \cdot 4}{6 \cdot 4}+\dfrac{23 \cdot 3}{8 \cdot 3}=\dfrac{44}{24}+\dfrac{69}{24}=\dfrac{113}{24}=4\dfrac{17}{24} }\)
3) \( \dfrac{3}{2} \, + \, 12 \, = \, \dfrac{3}{2} \, + \, \dfrac{24}{2} \, = \, \dfrac{27}{2}\, = \, 13 \dfrac{1} {2} \)
4) \(\dfrac{9}{11} \, + \, \dfrac{3}{4} \, = \, \dfrac{9\cdot 4}{11\cdot 4} \, + \, \dfrac{3\cdot 11}{4\cdot 11} \, = \, \dfrac{36}{44} \, + \, \dfrac{33}{44} \, = \, \dfrac{69}{44} \, = \, 1\dfrac{25}{44} \)
5) \( \dfrac{1}{7} \, - \, \dfrac{3}{5} \, = \, \dfrac{1 \cdot 5}{7 \cdot 5} \, - \, \dfrac{3 \cdot 7}{5 \cdot 7} \, = \, \dfrac{5}{35} \, - \, \dfrac{21}{35} \, = \, - \dfrac{16}{35} \)
6) \(11 \, - \, \dfrac{13}{3} \, = \, \dfrac{33}{3} \, - \, \dfrac{13}{3} \, = \, \dfrac{20}{3} \, = \, 6\dfrac{2}{3} \)
7) \({4 \dfrac{2}{9} \, - \, 1 \dfrac{1}{3} \, = \, \dfrac{36}{9} \, + \, \dfrac{2}{9} \, - \, \left( \dfrac{3}{3} \, + \, \dfrac{1}{3} \right) \, = \, \dfrac{38}{9} \, - \, \dfrac{4}{3} \, = \, \dfrac{38}{9} \, - \, \dfrac{4 \cdot 3}{3 \cdot 3} \, = \, \dfrac{38}{9} \, - \, \dfrac{12}{9} \, = \, \dfrac{26}{9} \, = \, 2 \dfrac{8}{9}}\)
8) \( -\dfrac{20}{7} \, - \, \dfrac{7}{10} \, = \, -\dfrac{20\cdot 10}{7\cdot 10} \, -\, \dfrac{7\cdot 7}{10\cdot 7} \, =\, -\dfrac{200}{70} \, - \, \dfrac{49}{70} \, = \, -\dfrac{249}{70} \, = \, -3\dfrac{39}{70}\)
9) \(\dfrac{42}{5} \, \cdot \, \dfrac{10}{63} \, = \, \dfrac{2}{1} \, \cdot \, \dfrac{2}{3} \, = \, \dfrac{4}{3} \, = \, 1\dfrac{1}{3} \)
Bemerkung: Vor dem Multiplizieren wurden hier die \(42\) (Zähler vom ersten Faktor) mit der \(63\) (Nenner vom zweiten Faktor) durch \(21\) sowie die \(5\) (Nenner vom ersten Faktor) mit der \(10\) (Zähler vom zweiten Faktor) durch \(5\) gekürzt. Das Kürzen kann natürlich auch schrittweise (z. B. erst durch \(7\) und dann durch \(3\) - kleines Einmaleins!) erfolgen, wenn man nicht sofort sieht, dass die \(21\) sowohl in der \(42\) als auch in der \(63\) enthalten ist.
10) \( \dfrac{7}{9} \, \cdot \, 6 \, = \, \dfrac{7}{9} \, \cdot \, \dfrac{6}{1} \, = \, \dfrac{7}{3} \, \cdot \, \dfrac{2}{1} \, = \, \dfrac{14}{3} \, = \, 4 \dfrac{2}{3}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(9\) (Nenner vom ersten Faktor) mit der \(6\) (Zähler vom zweiten Faktor) durch \(3\) gekürzt.
11) \(34 \, \cdot \, \dfrac{1}{2} \, = \, \dfrac{34}{2} \, = \, 17 \)
12) \(2\dfrac{1}{4} \, \cdot \, \dfrac{2}{7} \, = \, \dfrac{9}{4} \, \cdot \, \dfrac{2}{7} \, = \, \dfrac{9}{2} \, \cdot \, \dfrac{1}{7} \, = \, \dfrac{9}{14}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(4\) (Nenner vom ersten Faktor) mit der \(2\) (Zähler vom zweiten Faktor) durch \(2\) gekürzt.
13) \( \dfrac{3}{8} \, : \, \dfrac{5}{4} \, = \, \dfrac{3}{8} \, \cdot \, \dfrac{4}{5} \, = \, \dfrac{3}{2} \, \cdot \, \dfrac{1}{5} \, = \, \dfrac{3}{10} \)
Bemerkung: Vor dem Multiplizieren wurden hier die \(8\) (Nenner vom ersten Faktor) mit der \(4\) (Zähler vom zweiten Faktor) durch \(4\) gekürzt.
14) \( \dfrac{5}{6} \, : \, \dfrac{25}{12} \, = \, \dfrac{5}{6} \, \cdot \, \dfrac{12}{25} \, = \, \dfrac{1}{1} \, \cdot \dfrac{2}{5} \, = \, \dfrac {2}{5} \)
Bemerkung: Vor dem Multiplizieren wurden hier die \(5\) (Zähler vom ersten Faktor) mit der \(25\) (Nenner vom zweiten Faktor) durch \(5\) sowie die \(6\) (Nenner vom ersten Faktor) mit der \(12\) (Zähler vom zweiten Faktor) durch \(6\) gekürzt.
15) \(\dfrac{8}{9} : \dfrac{4}{27} = \dfrac{8}{9} \cdot \dfrac{27}{4} = 6 \)
Bemerkung: Vor dem Multiplizieren wurden hier die \(8\) (Zähler vom ersten Faktor) mit der \(4\) (Nenner vom zweiten Faktor) durch \(4\) sowie die \(9\) (Nenner vom ersten Faktor) mit der \(27\) (Zähler vom zweiten Faktor) durch \(9\) gekürzt.
16) \({4\dfrac{2}{5} \, : \, 3\dfrac{1}{10} \, = \, \left(\dfrac{20}{5}\, +\, \dfrac{2}{5}\right) \, : \, \left(\dfrac{30}{10}\, +\, \dfrac{1}{10}\right) \, =\, \dfrac{22}{5} \, : \, \dfrac{31}{10} \, = \, \dfrac{22}{5} \, \cdot \, \dfrac{10}{31} \, = \, \dfrac{44}{31} = 1\dfrac {13}{31}}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(5\) (Nenner vom ersten Faktor) mit der \(10\) (Zähler vom zweiten Faktor) durch \(5\) gekürzt.
17) \(4 \, - \, \dfrac{2}{3} \, \cdot \, \dfrac{5}{8} \, = \, 4 \, - \, \dfrac{1}{3} \, \cdot \, \dfrac{5}{4} \, = \,\dfrac{16}{4} \, - \, \dfrac{5}{12} \, = \, \dfrac{48}{12} \, - \, \dfrac{5}{12} \, = \, \dfrac{43}{12} \, = \, 3\dfrac{7}{12}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(2\) (Zähler vom ersten Faktor) mit der \(8\) (Nenner vom zweiten Faktor) durch \(2\) gekürzt.
18) \({ \dfrac{1}{2} \, + \, 5 \, : \, \dfrac{10}{13} \, + \, 2\dfrac{1}{8} \, = \, \dfrac{1}{2} \, + \, 5 \, \cdot \, \dfrac{13}{10} \, + \, \dfrac{16}{8} \, + \, \dfrac{1}{8} \, = \, \dfrac{1}{2} \, + \, \dfrac{13}{2} \, + \, \dfrac{17}{8} \, = \, \dfrac{4}{8} \, + \, \dfrac{52}{8} \, + \, \dfrac{17}{8} \, = \, \dfrac{73}{8} \, = \, 9\dfrac{1}{8} }\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(5\) (erster Faktor) mit der \(10\) (Nenner vom zweiten Faktor) durch \(5\) gekürzt.
19) \({\dfrac{13}{7} \, : \, \left(-\dfrac{26}{21}\right) \, \cdot \, \dfrac{8}{27} \, = \, \dfrac{13}{7} \, \cdot \, \left(-\dfrac{21}{26}\right) \, \cdot \, \dfrac{8}{27} \, = \, \dfrac{1}{1} \, \cdot \, \left(-\dfrac{3}{2}\right) \, \cdot \, \dfrac{8}{27} \, = \, 1 \, \cdot \, \left(-\dfrac{1}{1}\right) \, \cdot \, \dfrac{4}{9} \, = \, -\dfrac{4}{9} }\)
Bemerkung: Vor dem Multiplizieren wurden hier der Übersichtlichkeit wegen in zwei Schritten gekürzt:
1. Es wurden die \(13\) (Zähler vom ersten Faktor) mit der \(26\) (Nenner vom zweiten Faktor) durch \(13\) sowie die \(7\) (Nenner vom ersten Faktor) mit der \(21\) (Zähler vom zweiten Faktor) durch \(7\) gekürzt.
2. Es wurden die \(3\) (Zähler vom gekürzten zweiten Faktor) mit der \(27\) (Nenner vom dritten Faktor) durch \(3\) sowie die \(2\) (Nenner vom gekürzten zweiten Faktor) mit der \(8\) (Zähler vom dritten Faktor) durch \(2\) gekürzt.
20) \({-\dfrac{3}{2} \, + \, \dfrac{15}{4} \, \cdot \, \left(-\dfrac{16}{5}\right) \, - \, \dfrac{9}{6} \, : \, \left(-3\right) \, = \, -\dfrac{3}{2} \, + \, \dfrac{15}{4} \, \cdot \, \left(-\dfrac{16}{5}\right) \, - \, \dfrac{9}{6} \, \cdot \, \left(-\dfrac{1}{3}\right) \, = \, -\dfrac{3}{2} \, + \, \dfrac{3}{1} \, \cdot \, \left(-\dfrac{4}{1}\right) -\dfrac{3}{6}\, \cdot \, \left(-\dfrac{1}{1}\right) \, = \, -\dfrac{3}{2} \,- \, 12 \, + \, \dfrac{1}{2} \, = \, -\dfrac{26}{2} \, = \, -13 }\)
Bemerkung: Vor dem Multiplizieren wurden hier in beiden Produkten gekürzt:
1. Produkt: Es wurden die \(15\) (Zähler vom ersten Faktor) mit der \(5\) (Nenner vom zweiten Faktor) durch \(5\) sowie die \(4\) (Nenner vom ersten Faktor) mit der \(16\) (Zähler vom zweiten Faktor) durch \(4\) gekürzt.
2. Produkt: Es wurden die \(9\) (Zähler vom ersten Faktor) mit der \(3\) (Nenner vom zweiten Faktor) durch \(3\) gekürzt.
7. Aufgabe
1) \(\genfrac{}{}{1pt}{0}{\frac{3}{2}}{\frac{7}{3}} = \dfrac{3}{2} : \dfrac{7}{3} = \dfrac{3}{2} \cdot \dfrac{3}{7} = \dfrac{9}{14}\)
2) \(\genfrac{}{}{1pt}{0} {\frac{-5}{-3}}{-\frac{25}{4}} = \dfrac{-5}{-3} : \left( -\dfrac{25}{4} \right) = \dfrac{5}{3} \cdot \left( -\dfrac{4}{25} \right) = \dfrac{1}{3} \cdot \left( -\dfrac{4}{5} \right) = - \dfrac {4}{15}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(5\) (Zähler vom ersten Faktor) mit der \(25\) (Nenner vom zweiten Faktor) durch \(5\) gekürzt.
3) \(\genfrac{}{}{1pt}{0}{-15}{\frac{11}{-30}} = -15 : \left(\dfrac{11}{-30} \right) = -15 \cdot \left(-\dfrac{30}{11} \right) = \dfrac{450}{11}\)
4) \(\genfrac{}{}{1pt}{0}{\frac{8}{12}}{5} = \dfrac{8}{12} : \dfrac{5}{1} = \dfrac{8}{12} \cdot \dfrac{1}{5} = \dfrac{2}{15}\)
5) \(\genfrac{}{}{1pt}{0}{\frac{38}{-3}}{\frac{19}{4}} = \dfrac{38}{-3} : \dfrac{19}{4} = -\dfrac{38}{3} \cdot \dfrac{4}{19} = -\dfrac{2}{3} \cdot \dfrac{4}{1} = -\dfrac{8}{3}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(38\) (Zähler vom ersten Faktor) mit der \(19\) (Nenner vom zweiten Faktor) durch \(19\) gekürzt.
6) \(\genfrac{}{}{1pt}{0}{\frac{27}{16}}{\frac{3}{11}} = \dfrac{27}{16} : \dfrac{3}{11} = \dfrac{27}{16} \cdot \dfrac{11}{3} = \dfrac{9}{16} \cdot \dfrac{11}{1} = \dfrac{99}{16}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(27\) (Zähler vom ersten Faktor) mit der \(3\) (Nenner vom zweiten Faktor) durch \(3\) gekürzt.
7) \(\genfrac{}{}{1pt}{0}{113}{\frac{17}{2}} = 113 : \dfrac{17}{2} = 113 \cdot \dfrac{2}{17} = \dfrac{226}{17}\)
8) \(\genfrac{}{}{1pt}{0}{\frac{-42}{5}}{102} = \dfrac{-42}{5} : \dfrac{102}{1} = -\dfrac{42}{5} \cdot \dfrac{1}{102} = -\dfrac{7}{5} \cdot \dfrac{1}{17} = -\dfrac{7}{85}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(42\) (Zähler vom ersten Faktor) mit der \(102\) (Nenner vom zweiten Faktor) durch \(6\) gekürzt.
9) \(\genfrac{}{}{1pt}{0}{-\frac{1}{9}}{\frac{1}{81}} = -\dfrac{1}{9} : \dfrac{1}{81} = -\dfrac{1}{9} \cdot \dfrac{81}{1} = -\dfrac{1}{1} \cdot \dfrac{9}{1} = -9\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(9\) (Nenner vom ersten Faktor) mit der \(81\) (Zähler vom zweiten Faktor) durch \(9\) gekürzt.
10) \(\genfrac{}{}{1pt}{0}{\frac{14}{23}}{-6} = \dfrac{14}{23} : \left(-\dfrac{6}{1} \right) = \dfrac{14}{23} \cdot \left(-\dfrac{1}{6} \right) = \dfrac{7}{23} \cdot \left( -\dfrac{1}{3} \right) = -\dfrac{7}{69}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(14\) (Zähler vom ersten Faktor) mit der \(6\) (Nenner vom zweiten Faktor) durch \(2\) gekürzt.
11) \(\genfrac{}{}{1pt}{0}{-\frac{21}{8}}{-\frac{12}{5}} = -\dfrac{21}{8} : \left(-\dfrac{12}{5} \right) = -\dfrac{21}{8} \cdot \left(-\dfrac{5}{12} \right) = -\dfrac{7}{8} \cdot \left( -\dfrac{5}{4} \right) = \dfrac{35}{32}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(21\) (Zähler vom ersten Faktor) mit der \(12\) (Nenner vom zweiten Faktor) durch \(3\) gekürzt.
12) \(\genfrac{}{}{1pt}{0}{-34}{\frac{-43}{-12}} = -34 : \left(\dfrac{-43}{-12}\right) = -34 \cdot \dfrac{12}{43} = -\dfrac{408}{43}\)
13) \(\genfrac{}{}{1pt}{0}{\frac{-5}{72}}{\frac{-40}{11}} = \dfrac{-5}{72} : \dfrac{-40}{11} = -\dfrac{5}{72} \cdot \left(-\dfrac{11}{40}\right) = -\dfrac{1}{72} \cdot \left(-\dfrac{11}{8}\right) = \dfrac{11}{576}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(5\) (Zähler vom ersten Faktor) mit der \(40\) (Nenner vom zweiten Faktor) durch \(5\) gekürzt.
14) \(\genfrac{}{}{1pt}{0}{\frac{5}{4}}{-\frac{21}{52}} = \dfrac{5}{4} : \left(-\dfrac{21}{52}\right) = \dfrac{5}{4} \cdot \left(-\dfrac{52}{21}\right) = \dfrac{5}{1} \cdot \left( -\dfrac{13}{21} \right) = -\dfrac{65}{21}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(4\) (Nenner vom ersten Faktor) mit der \(52\) (Zähler vom zweiten Faktor) durch \(4\) gekürzt.
15) \(\genfrac{}{}{1pt}{0}{\frac{19}{15}}{\frac{-7}{102}} = \dfrac{19}{15} : \dfrac{-7}{102} = \dfrac{19}{15} \cdot \left(-\dfrac{102}{7}\right) = \dfrac{19}{5} \cdot \left(-\dfrac{34}{7}\right) = -\dfrac{646}{35}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(15\) (Nenner vom ersten Faktor) mit der \(102\) (Zähler vom zweiten Faktor) durch \(3\) gekürzt.
16) \(\genfrac{}{}{1pt}{0}{\frac{-33}{16}}{-\frac{99}{14}} = -\dfrac{33}{16} : \left(-\dfrac{99}{14}\right) = -\dfrac{33}{16} \cdot \left(-\dfrac{14}{99}\right) = -\dfrac{1}{8} \cdot \left(-\dfrac{7}{3}\right) = \dfrac{7}{24}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(33\) (Zähler vom ersten Faktor) mit der \(99\) (Nenner vom zweiten Faktor) durch \(33\) sowie die \(16\) (Nenner vom ersten Faktor) mit der \(14\) (Zähler vom zweiten Faktor) durch \(2\) gekürzt.
17) \(-\genfrac{}{}{1pt}{0}{-\frac{121}{17}}{\frac{77}{170}} = -\left(-\dfrac{121}{17} : \dfrac{77}{170}\right) = -\left(-\dfrac{121}{17} \cdot \dfrac{170}{77}\right) = -\left(-\dfrac{11}{1} \cdot \dfrac{10}{7}\right) = \dfrac{110}{7}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(121\) (Zähler vom ersten Faktor) mit der \(77\) (Nenner vom zweiten Faktor) durch \(11\) sowie die \(17\) (Nenner vom ersten Faktor) mit der \(170\) (Zähler vom zweiten Faktor) durch \(17\) gekürzt.
18) \(\genfrac{}{}{1pt}{0}{\frac{142}{27}}{\frac{71}{72}} = \dfrac{142}{27} : \dfrac{71}{72} = \dfrac{142}{27} \cdot \dfrac{72}{71} = \dfrac{2}{3} \cdot \dfrac{8}{1} = \dfrac{16}{3}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(142\) (Zähler vom ersten Faktor) mit der \(71\) (Nenner vom zweiten Faktor) durch \(71\) sowie die \(27\) (Nenner vom ersten Faktor) mit der \(72\) (Zähler vom zweiten Faktor) durch \(9\) gekürzt.
19) \(\genfrac{}{}{1pt}{0}{\frac{2}{15}}{\frac{-46}{-65}} = \dfrac{2}{15} : \dfrac{-46}{-65} = \dfrac{2}{15} \cdot \dfrac{65}{46} = \dfrac{1}{3} \cdot \dfrac{13}{23} = \dfrac{13}{69}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(2\) (Zähler vom ersten Faktor) mit der \(46\) (Nenner vom zweiten Faktor) durch \(2\) sowie die \(15\) (Nenner vom ersten Faktor) mit der \(65\) (Zähler vom zweiten Faktor) durch \(5\) gekürzt.
20) \(\genfrac{}{}{1pt}{0}{-\frac{25}{256}}{-\frac{225}{32}} = -\dfrac{25}{256} : \left(-\dfrac{225}{32}\right) = -\dfrac{25}{256} \cdot \left(-\dfrac{32}{225}\right) = -\dfrac{1}{8} \cdot \left(-\dfrac{1}{9}\right) = \dfrac{1}{72}\)
Bemerkung: Vor dem Multiplizieren wurden hier die \(25\) (Zähler vom ersten Faktor) mit der \(225\) (Nenner vom zweiten Faktor) durch \(25\) sowie die \(256\) (Nenner vom ersten Faktor) mit der \(32\) (Zähler vom zweiten Faktor) durch \(32\) gekürzt.
8. Aufgabe
Schreibt man die Rechnung mit Brüchen auf, kommt man mit viel Kürzen, dafür wenig Rechnen, zum Ergebnis:
\(\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot\dfrac{4}{5}\cdot\dfrac{5}{6}\cdot\dfrac{6}{7}\cdot\dfrac{7}{8}\cdot\dfrac{8}{9}\cdot\dfrac{9}{10}\cdot 10 = 1\)
An dieser Aufgabe wird auch offensichtlich, warum Brüche häufig einen Vorteil gegenüber Dezimalzahlen haben. Bei
\(0{,}5\cdot 0{,}666\ldots\cdot 0{,}75\cdot 0{,}8\cdot 0{,}833\ldots\cdot 0{,}857\ldots\cdot 0{,}875\cdot 0{,}888\ldots\cdot 0{,}9\cdot 10 = 1\)
wäre die Logik der Rechnung nämlich nicht so deutlich wie oben. Mal abgesehen davon, dass Rundungsfehler meist dazu führen werden, dass die Lösung nicht exakt \(1\) ist.
9. Aufgabe
Bemerkung 1: Grundsätzlich sind diese Aufgaben nicht eindeutig zu lösen. Neben der Anforderung, dass die Rechnungen stimmen sollen, ist daher die Vorgabe, dass möglichst kleine Ziffern gefunden werden sollen, entscheidend. Ein bisschen "Rumprobieren" wird aber auch so nötig sein.
Bemerkung 2: Auch wenn z. B. im Zähler "nur" ein Sternchen steht, muss dieses beim Erweitern mit der entsprechenden Zahl multipliziert werden, weil erweitern nun mal heißt "Zähler und Nenner mit der gleichen Zahl multiplizieren". Das gilt auch für Sternchen!
1)
Überlegung: Damit eine Differenz \(0\) ergibt, müssen Minuend und Subtrahend gleich sein. Die naheliegendste Lösung ist also \(\dfrac{28}{11}-\dfrac{28}{11} \, = \, 0\)
Bemerkung: Dies ist aber nicht die einzige Lösung, z. B. stimmt auch \(\dfrac{14}{11}-\dfrac{28}{22} \, = \, 0\). Und es kann noch nicht mal entschieden werden, welche Zahlenkombination die kleinere ist ...
2)
1. Überlegung: Da beim Multiplizieren von Brüchen jeweils die Zähler und die Nenner multipliziert werden, können sie separat betrachtet werden.
2. Überlegung: Im Nenner muss einfach nur multipliziert werden: \(3 \cdot 8=24\), also ist \(\dfrac{*}{3}\cdot \dfrac{*}{8} \, = \, \dfrac{35}{24}\)
3. Überlegung: Die \(35\) im Zähler des Bruches auf der rechten Seite kann im Bereich der natürlichen Zahlen nur auf genau eine Weise in Faktoren zerlegt werden, nämlich \(35=5 \cdot 7\). Es kann allerdings nicht entschieden werden, welcher Faktor an erster und welcher Faktor an zweiter Stelle in der ursprünglichen Rechnung steht. Es gibt daher zwei Lösungen.
Lösung: \(\dfrac{5}{3}\cdot \dfrac{7}{8} \, = \, \dfrac{35}{24}\) oder \(\dfrac{7}{3}\cdot \dfrac{5}{8} \, = \, \dfrac{35}{24}\)
3)
1. Überlegung: Einfacher wird die Rechnung, wenn die gemischte Zahl auf der rechten Seite in einen unechten Bruch umgewandelt wird. Es ergibt sich: \(\dfrac{5}{*}+\dfrac{*}{5} \, = \, \dfrac{49}{10}\)
2. Überlegung: Die kleinste Ziffer, die für den Nenner des ersten Bruches infrage kommt, ist \(1\). \(0\) scheidet ja als Kandidat für einen Nenner aus. Er ergibt sich: \(\dfrac{5}{1}+\dfrac{*}{5} \, = \, \dfrac {49}{10}\)
3. Überlegung: Das lässt sich umformen zu \(\dfrac{*}{5} \, = \, \dfrac {49}{10}-5\) oder \(\dfrac{*}{5} \, = \, -\dfrac{1}{10}\). Dies ist (mathematisch gesprochen) die Frage, welche Zahl ergibt \(-\dfrac{1}{10}\), wenn man sie durch \(5\) teilt. Eigentlich muss man an dieser Stelle gar nicht weiterrechnen, weil nur eine negative Zahl hier für ein richtiges Ergebnis sorgen kann: Eine positive Zahl geteilt durch eine andere positive Zahl (und die \(5\) ist ja hier als positive Zahl schon vorgegeben) wäre ja wieder positiv und nicht \(-\dfrac{1}{10}\). Damit kann man die Vorgabe, dass für die Sternchen Ziffern eingesetzt werden sollen, nie erfüllen. Für diejenigen, die das genaue Ergebnis in diesem Fall wissen möchten: Für das Sternchen müsste \(-\dfrac{1}{2}\) eingesetzt werden, damit die Rechnung stimmt, was auch deswegen nicht funktioniert, weil es nicht ganzzahlig ist.
4. Überlegung: Probieren wir es also mit der nächstgrößeren Ziffer \(2\). Wir bekommen: \(\dfrac{5}{2}+\dfrac{*}{5} \, = \, \dfrac{49}{10}\) oder (wenn wir alles auf den Hauptnenner bringen) \(\dfrac{25}{10}+\dfrac{2\cdot *}{10} \, = \, \dfrac{49}{10}\)
5. Überlegung: Da die Nenner nun gleich sind, können wir sie für den folgenden Schritt ignorieren. Es ergibt sich: \(25+2\cdot *=49\). Daraus folgt: \(2 \cdot *=24\) und damit \(*=12\)
Lösung: \(\dfrac{5}{2}+\dfrac{12}{5} \, = \, 4\dfrac{9}{10}\)
4)
1. Überlegung: Das Sternchen auf der rechten Seite muss für \(45\) stehen, da dies der Hauptnenner von \(5\) und \(9\) ist. Es ergibt sich: \(\dfrac{1}{5}-\dfrac{*}{9} \, = \, -\dfrac{1}{45}\) oder, wenn man gleich alles auf den Hauptnenner bringt, \(\dfrac{9}{45}-\dfrac{5\cdot *}{45} \, = \, -\dfrac{1}{45}\)
2. Überlegung: Da die Nenner nun gleich sind, können wir sie wieder ignorieren. Bleibt die Frage: \(9-5\cdot *=-1\), die uns zu der Erkenntnis führt, dass \(5\cdot *\) offensichtlich gleich \(10\) sein muss. Wenn \(5 \cdot *=10\) ist, ist \(*=2\)
Lösung: \(\dfrac{9}{45}-\dfrac{10}{45} \, = \, -\dfrac{1}{45}\) oder \(\dfrac{1}{5}-\dfrac{2}{9} \, = \, -\dfrac{1}{45}\)
5)
1. Überlegung: Auf der rechten Seite hat das Sternchen im Nenner keine Auswirkungen auf die Rechnung, egal durch welche Zahl die \(0\) im Zähler geteilt wird, das Ergebnis ist immer \(0\); mit Ausnahme der \(0\) selbst, denn \(\frac{0}{0}\) ist nicht definiert. Da eine möglichst kleine Ziffer gefordert war, können wir die \(1\) für dieses Sternchen nehmen - oder es einfach weglassen.
2. Überlegung: Damit das Ergebnis insgesamt \(0\) ist, müsste auf der linken Seite eine der Zahlen negativ sein, denn die Summe von zwei positiven Zahlen ist wieder positiv. Negative Zahlen haben wir aber wegen der Einschränkung, dass Ziffern gesucht sind, nicht zur Verfügung. Insofern lassen sich hier keine passenden Zahlen finden.
6)
1. Überlegung: Man teilt durch einen Bruch, indem man mit dem Kehrwert multipliziert. Das bedeutet hier: \(\dfrac{5}{*1} \cdot \dfrac{*}{2} \, = \, \dfrac{5}{2*}\)
2. Überlegung: Schauen wir uns die Rechnung im Zähler an: \(5\cdot *=5\). Also muss dieses Sternchen gleich \(1\) sein. Es ergibt sich: \(\dfrac{5}{*1} \cdot \dfrac{1}{2} \, = \, \dfrac{5}{2*}\) bzw. in der Originalrechnung: \(\dfrac{5}{*1} : \dfrac{2}{1} \, = \, \dfrac{5}{2*}\)
3. Überlegung: Für den Nenner folgt daraus: \(*1\cdot 2=2*\). Für das rechte Sternchen berechnet man \(1 \cdot 2 = 2\); für das linke umgekehrt. Das Ergebnis ist also \(11\cdot 2=22\)
Lösung: \(\dfrac{5}{11} : \dfrac{2}{1} \, = \, \dfrac{5}{22}\) bzw. \(\dfrac{5}{11} : 2 \, = \, \dfrac{5}{22}\), was man natürlich auch dafür schreiben kann
Die Urheber dieses Werkes veröffentlichen es unter folgender Lizenz:

Lernmodul Mathematik von Dr. Xenia V. Jeremias/Technische Hochschule Wildau/Hochschule für nachhaltige Entwicklung Eberswalde ist lizenziert unter einer Creative Commons Namensnennung - Nicht-kommerziell - Weitergabe unter gleichen Bedingungen 4.0 International Lizenz
Sie dürfen:
- Teilen - das Material in jedwedem Format oder Medium vervielfältigen und weiterverbreiten
- Bearbeiten - das Material remixen, verändern und darauf aufbauen
Zu den folgenden Bedingungen:
- Namensnennung - Sie müssen angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade Sie oder Ihre Nutzung besonders.
Das bedeutet für dieses Lernmodul: Neben dem Namen der Autorin Xenia V. Jeremias müssen die beiden Einrichtungen Technische Hochschule Wildau und Hochschule für nachhaltige Entwicklung Eberswalde genannt werden. - Nicht kommerziell - Sie dürfen das Material nicht für kommerzielle Zwecke nutzen.
- Weitergabe unter gleichen Bedingungen - Wenn Sie das Material remixen, verändern oder anderweitig direkt darauf aufbauen, dürfen Sie Ihre Beiträge nur unter derselben Lizenz wie das Original verbreiten.
- Keine weiteren Einschränkungen - Sie dürfen keine zusätzlichen Klauseln oder technische Verfahren einsetzen, die anderen rechtlich irgendetwas untersagen, was die Lizenz erlaubt.