Die andere Größe, die die Geschwindigkeit des Schiffes bestimmt, ist die sogenannte STOKESsche (George Gabriel STOKES, 1819-1903) oder viskose Reibung. Dies ist eine der Bewegungsrichtung entgegengesetzte Kraft, die immer dann auftritt, wenn sich ein Körper nicht zu schnell durch eine Flüssigkeit oder ein Gas bewegt. Die Kraft ist insbesondere von der Geschwindigkeit, aber auch von der Form und der Größe des Körpers sowie der jeweiligen Flüssigkeit bzw. dem Gas abhängig. Die Messung von Geschwindigkeit und Reibungskraft bei einem Schiff ergab die folgende Wertetabelle.
a) Begründe, dass der Zusammenhang zwischen der Geschwindigkeit und der Reibungskraft durch eine Lineare Funktion beschrieben werden kann.
✅ Lösung
Wenn sich die Geschwindigkeit jeweils um \(1\,\frac{\rm{km}}{\rm{h}}\) vergrößert, so vergrößert sich die Reibungskraft immer um den gleichen Wert von \(500\,\rm{N}\). Außerdem muss aus physikalischen Gründen die Reibungskraft immer weiter zunehmen.
b) Bestimme mit Hilfe von zwei Wertepaaren den Funktionsterm dieser Linearen Funktion.
✅ Lösung
fr(v):=m·v+n → 500·v
linSolve({2000=fr(4),4000=fr(8)},{m,n})
m:=500
n:=0
fr(v)
c) Überprüfe, ob die anderen gemessenen Wertepaare die Funktionsgleichung dieser Linearen Funktion erfüllen.
d) Zeichne den Graphen dieser Linearen Funktion in das Koordinatensystem aus Aufgabenteil 1.d ein.
✅ Lösung
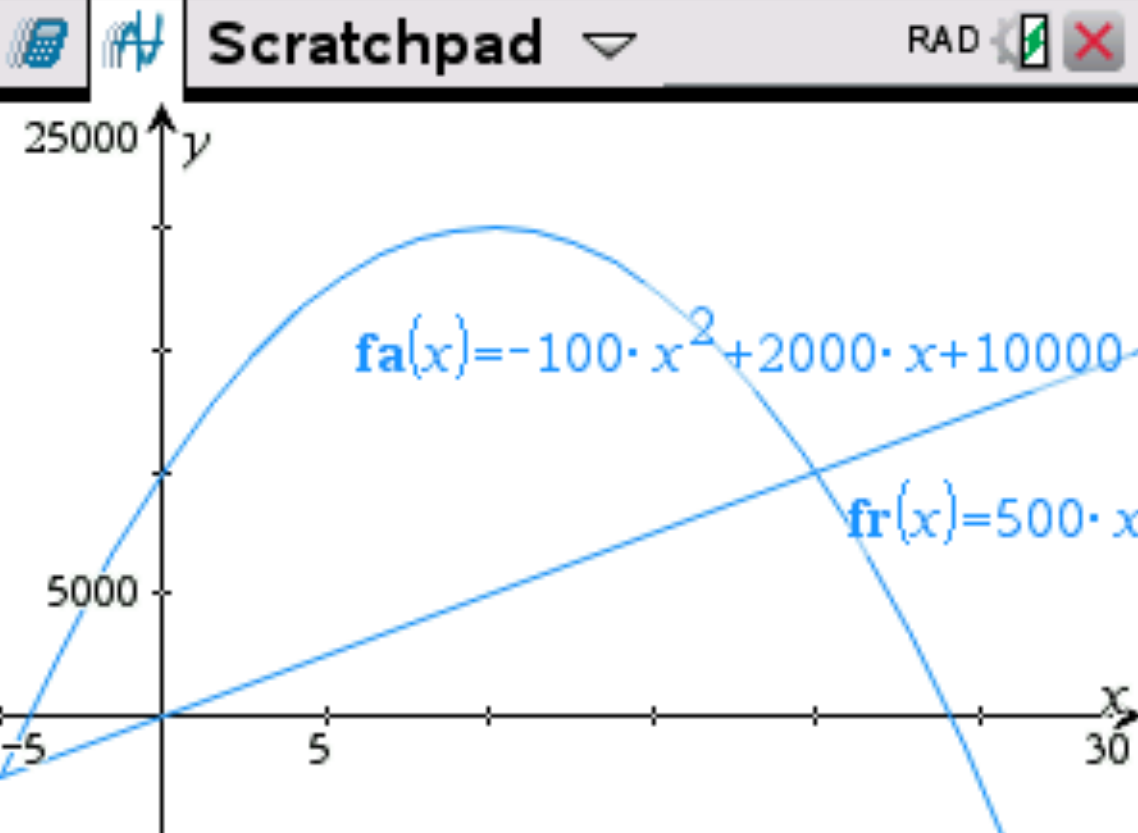
e) Berechne die Reibungskraft bei einer Geschwindigkeit von \(15\,\frac{\rm{km}}{\rm{h}}\).
✅ Lösung
fr(15) → 7500
Bei einer Geschwindigkeit von \(15\,\frac{\rm{km}}{\rm{h}}\) beträgt die Reibungskraft \(7500\,\rm{N}\).
f) Berechne die Geschwindigkeit bei einer Reibungskraft von \(6250\,\rm{N}\).
✅ Lösung
solve(fr(v)=6250,v) → \(v=\frac{25}{2}\)Ans⏵Decimal → v=12.5
Die Reibungskraft beträgt \(6250\,\rm{N}\) bei der Geschwindigkeit \(12{,}5\,\frac{\rm{km}}{\rm{h}}\).