Zuerst nimmt der Falkner aus seiner Tasche einen Fleischbrocken und wirft diesen senkrecht in die Höhe. Die Messung von Zeit und Höhe des Fleischbrockens ergab die folgende Wertetabelle.
a) Begründe, dass der Zusammenhang zwischen der Zeit und der Höhe nicht durch eine Lineare Funktion beschrieben werden kann.
✅ Lösung
Wenn sich die Zeit jeweils um \(0{,}1\,\rm{s}\) vergrößert, so vergrößert sich die Höhe nicht immer um den gleichen Wert. Außerdem muss aus physikalischen Gründen die Höhe irgendwann wieder abnehmen.
Wir nehmen an, dass der Zusammenhang zwischen der Zeit und der Höhe durch eine Quadratische Funktion beschrieben werden kann.
b) Bestimme mit Hilfe von drei Wertepaaren den Funktionsterm dieser Quadratischen Funktion.
✅ Lösung
hf(t):=a·t²+b·t+c → -5·t²+10·t+1.5
linSolve({4.05=hf(0.3),5.25=hf(0.5),6.05=hf(0.7)},{a,b,c})
a:=-5
b:=10
c:=1.5
hf(t)
c) Überprüfe, ob die anderen gemessenen Wertepaare die Funktionsgleichung dieser Quadratischen Funktion erfüllen.
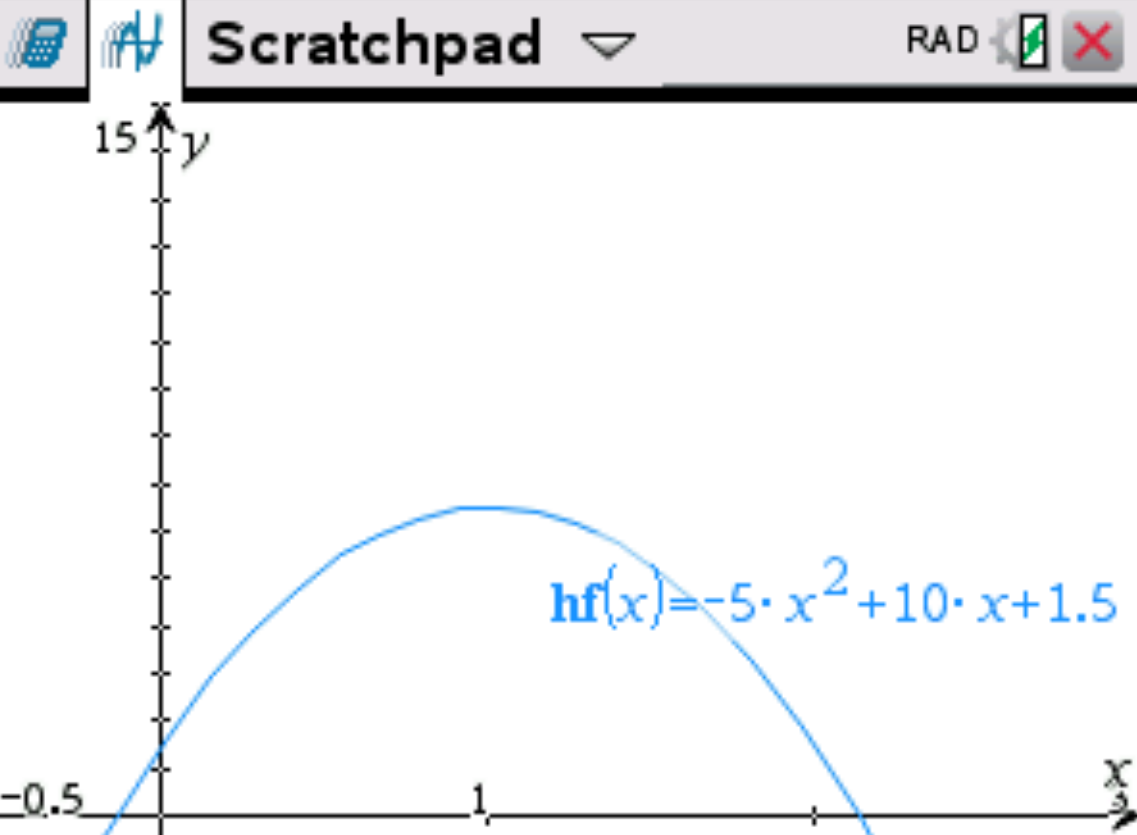
d) Zeichne den Graphen dieser Quadratischen Funktion in einem passenden Koordinatensystem.
✅ Lösung
e) Berechne die Höhe des Fleischbrockens zum Zeitpunkt \(1{,}9\,\rm{s}\).
✅ Lösung
hf(1.9) → 2.45
Zum Zeitpunkt \(1.9\,\rm{s}\) beträgt die Höhe \(2{,}45\,\rm{m}\).
f) Berechne den Zeitpunkt, zu dem der Fleischbrocken auf den Boden fällt.
✅ Lösung
zeros(hf(t),t) → {-0.140175,2.14018}
Auf den Boden trifft der Fleischbrocken nach ca. \(2{,}14\,\rm{s}\).
g) Berechne, zu welchem Zeitpunkt der Fleischbrocken die größte Höhe hat und wie groß diese Höhe ist.
✅ Lösung
completeSquare(hf(t),t) → 6.5-5·(t-1)²
Die größte Höhe hat der Fleischbrocken nach \(1\,\rm{s}\) mit \(6{,}5\,\rm{m}\).